Las Interpretaciones de la Mecánica Cuántica 🌟
En esta entrada del blog hablaremos, de nuevo, de mecánica cuántica. Sin embargo, esta vez no será como el resto. Hoy no hablaremos de fenómenos o experimentos, sino que nos centraremos en cómo se trata a la mecánica cuántica, cómo se interpreta y qué significado tiene para los físicos, es decir, veremos qué son Las interpretaciones de la Mecánica Cuántica.
Normalmente en ciencia las
teorías suelen ser únicas y los sucesos que describen, tangibles, concretos y
absolutos. Si una manzana cae de forma vertical, está claro que impactará en la
parte del suelo justo debajo de ella. Si observamos un coche que circula por la
carretera y pestañeamos, el coche seguirá su camino y seguiremos observándole
circular. Pero en la mecánica cuántica ocurren sucesos “imposibles” vistos con
los ojos de la física clásica. En por eso que para explicar dichos sucesos hay
que introducir nuevos conceptos y cambiar la forma que tenemos de pensar en
ciencia clásica.
Este comienzo se da en 1920, cuando Luis De Broglie introdujo la noción de dualidad onda-partícula, de la que ya hablamos en otras entradas (Experimento de la doble Rendija y Efecto Túnel) y que dota a la materia de propiedades ondulatorias y corpusculares simultáneamente. Esto unido con el modelo atómico vigente en la época (el de Bohr, del que hablaremos en el blog más adelante) dejaba muchos interrogantes tras de sí. Se necesitaba una teoría matemática completa que explicase todos estos fenómenos y con la que se pudiese operar para no solo medir, sino predecir los comportamientos de las partículas. Las dos personas que se encargaron de arrojar luz sobre esta cuestión fueron Schrödinger y Heissenberg, pero no conjuntamente. Ambos crearon dos teorías radicalmente distintas para explicar los mismos fenómenos y esto era algo novedoso y que por supuesto no era posible admitir. A lo largo de la entrada profundizaremos en estas teorías y cómo ha evolucionado esta dualidad
Teoría ondulatoria de Schrödinger
Erwin Schrödinger nació en 1887 en Viena, en el seno de una familia acomodada. Como tal, recibió educación por parte de su padre en casa, quien se encargó de inculcarle interés en la ciencia y en la búsqueda del conocimiento. Su vida académica ha estado marcada por la persecución nazi, por lo que recorrió europa huyendo de el régimen antisemita, ejerciendo en numerosas universidades como Oxford, Viena o Dublín.
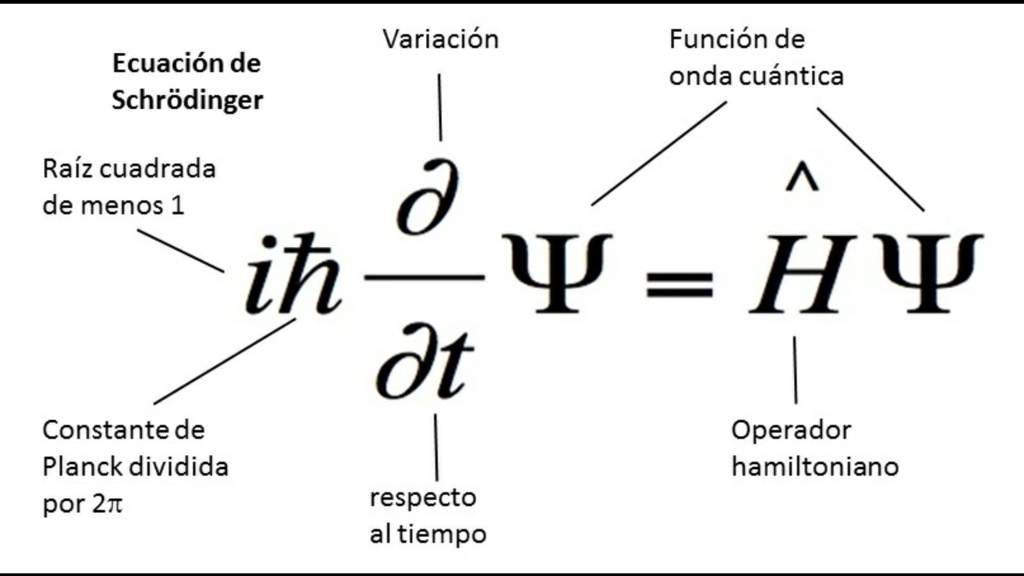
A Erwin se le ocurrió la idea de usar el concepto de De Broglie de dualidad onda-partícula: en vez de tratar al electrón como una partícula, pongamos nuestro punto de partida en la ecuación de onda clásica y adoptémosla al comportamiento cuántico que presentan las partículas subatómicas. Y así fue como en 1933 Schrödinger fue premiado con el premio Nobel por la formulación de la ecuación que lleva su nombre y con la que describe el comportamiento de partículas subatómicas. Se trata de una EDP (ecuación en derivadas parciales) donde la incógnita es la función de onda de la partícula en cuestión:
Posteriormente Max Born aportó una interpretación estadística de la función de onda como una función de densidad de probabilidad, lo cual solucionó el problema que planteaba este descubrimiento: ¿eran en realidad las partículas subatómicas una onda física? Actualmente esta función de onda se interpreta tan solo como un intervalo de probabilidades en las que es posible encontrar a la partícula.
Pero esto no acaba aquí porque aun hay que hablar del rival de Schrödinger: Heissenberg y su formulación matricial de la mecánica cuántica
Mecánica matricial de Heissenberg
Allí reflexionó acerca de los estudios que estaba llevando acabo Bohr y sobre las nuevas ideas emergentes en la física cuántica. Observó que, para poder dar una formulación matemática de la mecánica cuántica, no hacía falta poner el foco de atención en la estructura atómica en sí, sino en lo que el físico podía observar: las frecuencias y los espectros de emisión, asociados estos dos fenómenos a la teoría de Fourier. Todos estos datos venían dados matemáticamente por matrices (tablas de números) y aprender a manejarlas y a operar con ellas fue todo un reto para Heisenberg. Pero fue de esta forma como Heisenberg consiguió crear una teoría matemática para los sistemas cuánticos que, además, gozaba de una ventaja: no dependían en absoluto de la constante de Planck (que aparece en la función de onda). Gracias a esta mecánica, Heisenberg pudo obtener, por ejemplo, la energía del sistema del oscilador armónico.
Un debate que aún sigue abierto
Interpretación de los universos paralelos
Sostiene que, a pesar de que el observador solo mide 1 de todos los estados posibles, en realidad suceden todos los posibles sucesos, aunque en universos paralelos al nuestro con el que no interactuamos. Además, para esta interpretación la función de onda es un ente real y físico y asegura que el observador no ejerce ninguna influencia en el sistema. La interpretación de Copenhague niega lo primero y no tiene una respuesta clara para lo segundo. Sin embargo ambas coinciden en que no existen variables ocultas (parámetros desconocidos no descubiertos).
Interpretación de Bohm
Promovida por De Broglie y Bohm, sigue el camino de la interpretación anterior en cuanto al rol del observador y la tangibilidad de la función de onda, pero además afirma que existen variables ocultas que no hemos conseguido medir (habla de la verdadera dualidad física de las partículas subatómicas, siendo estas corpúsculos guiados por ondas guía)
Interpretación estadística
Planteada por Born, sostiene que los posibles estados cuánticos que puede tomar una partícula no son aleatorios, sino que son fluctuaciones ocasionadas por el entorno y que estas no son observables. Dichas fluctuaciones además siguen un patrón estadístico.
Espero que te haya gustado esta entrada y gracias por leerme una semana más!!!!.
La siguiente entrada continúa con la Saga Mujeres Extraordinarias, en la que hablaremos de la gran Agnesi 😁😁
Autora: Paola Diago




Un cordial saludo. Con respecto a "las interpretaciones y los problemas ontológicos de la Mecánica Cuántica", y teniendo en cuenta el reconocimiento académico que están logrando los Programas de Inteligencia Artificial en consultas de Física y Cosmología, les cuento que: se consultaron a 8 de estos programas sobre "el origen y significado ontológico de la unidad de medida de la constante de Planck", y resulta que todos coincidieron! en responder que "esta unidad de medida tiene implícito un término físico en su denominador, y que al ser considerado permite resolver las principales paradojas y deficiencias ontológicas de la Mecánica Cuántica"!. De manera que lo interesante de este tema es que: O bien se demuestra que todos estos programas se equivocaron! (lo que de por sí resultaría bastante trascendente) o por el contrario sus "deducciones" son correctas! Si les resulta de interés darle un "vistazo" a estos resultados, hacédmelo saber para enviarles los texto descriptivos. Atentamente, José Alberto (diazreyesjosealberto62@gmail.com)
ResponderEliminar